If cdef is a parallelogram find fcd – In the realm of geometry, parallelograms hold a distinct place, characterized by their unique properties and relationships. If CDEF is a parallelogram, determining the measure of angle FCD becomes a fundamental task. This guide will delve into the intricacies of parallelograms, providing a comprehensive approach to finding FCD.

The concept of parallelograms extends beyond mere definitions; it encompasses a tapestry of characteristics, properties, and angle relationships. Understanding these elements is essential for navigating the complexities of parallelogram geometry.

Definition of Parallelogram

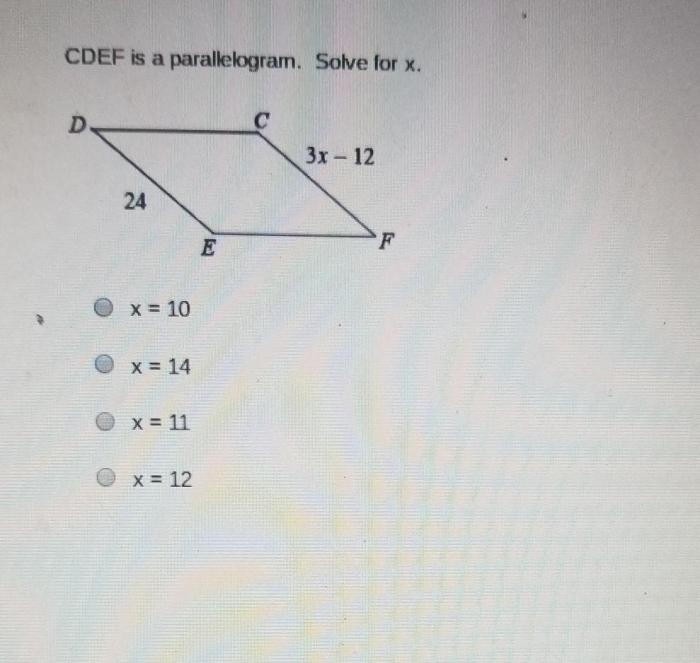
A parallelogram is a two-dimensional geometric shape with four sides and four angles. It is a special type of quadrilateral that has two pairs of parallel sides.

The key features that distinguish a parallelogram from other quadrilaterals are its parallel sides and opposite angles. The opposite sides of a parallelogram are congruent, and the opposite angles are equal. Additionally, the diagonals of a parallelogram bisect each other.

Properties of Parallelograms

• Opposite sides are parallel and congruent.
• Opposite angles are equal.
• Diagonals bisect each other.
• The sum of the interior angles is 360 degrees.
• The area of a parallelogram is equal to the product of its base and height.

Identifying Parallelograms

Determining whether a quadrilateral is a parallelogram requires careful examination of its properties. Parallelograms possess distinctive characteristics that set them apart from other quadrilaterals.

Properties of Parallelograms

Parallelograms are characterized by several key properties:

• Opposite Sides are Parallel:The opposite sides of a parallelogram are parallel to each other, forming two pairs of parallel lines.
• Opposite Angles are Congruent:The opposite angles of a parallelogram are congruent, meaning they have the same measure.
• Consecutive Angles are Supplementary:The consecutive angles of a parallelogram are supplementary, meaning they add up to 180 degrees.
• Diagonals Bisect Each Other:The diagonals of a parallelogram bisect each other, forming two congruent triangles.

Methods for Identifying Parallelograms

To determine if a quadrilateral is a parallelogram, several methods can be employed:

• Checking Opposite Sides and Angles:If the opposite sides of a quadrilateral are parallel and the opposite angles are congruent, then it is a parallelogram.
• Checking Consecutive Angles:If the consecutive angles of a quadrilateral are supplementary, then it is a parallelogram.
• Checking Diagonals:If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.

Examples of Parallelograms and Non-Parallelograms

Examples of parallelograms include rectangles, squares, and rhombuses. Non-parallelograms include trapezoids, kites, and general quadrilaterals.

Properties of Parallelograms: If Cdef Is A Parallelogram Find Fcd

Parallelograms possess distinct properties that define their geometric characteristics. These properties include:

Opposite Sides

• Opposite sides are parallel:The opposite sides of a parallelogram are always parallel to each other. This means that they never intersect, regardless of how far they are extended.
• Opposite sides are congruent:The opposite sides of a parallelogram are also congruent, meaning they have the same length. This implies that the parallelogram has two pairs of equal sides.

Diagonals, If cdef is a parallelogram find fcd

• Diagonals bisect each other:The diagonals of a parallelogram bisect each other, meaning they intersect at a point that divides both diagonals into two equal segments. This property is unique to parallelograms and is not shared by other quadrilaterals.

These properties collectively define the unique geometric shape of a parallelogram and distinguish it from other types of quadrilaterals.

Angle Relationships in Parallelograms

Parallelograms possess specific angle relationships that define their shape and characteristics. These relationships play a crucial role in understanding the geometry and properties of parallelograms.

One fundamental angle relationship in parallelograms is the congruence of opposite angles. Opposite angles are those that are located across the parallelogram from each other. For instance, in a parallelogram, the angles at one vertex are congruent to the angles at the opposite vertex.

Supplementary Angles

Another important angle relationship in parallelograms is the presence of supplementary angles. Supplementary angles are two angles whose sum is 180 degrees. In a parallelogram, the adjacent angles are supplementary. For example, the angles at one vertex of a parallelogram are adjacent and add up to 180 degrees.

These angle relationships are crucial for analyzing and solving problems involving parallelograms. They provide a foundation for understanding the geometry and properties of these shapes.

Finding FCD in a Parallelogram

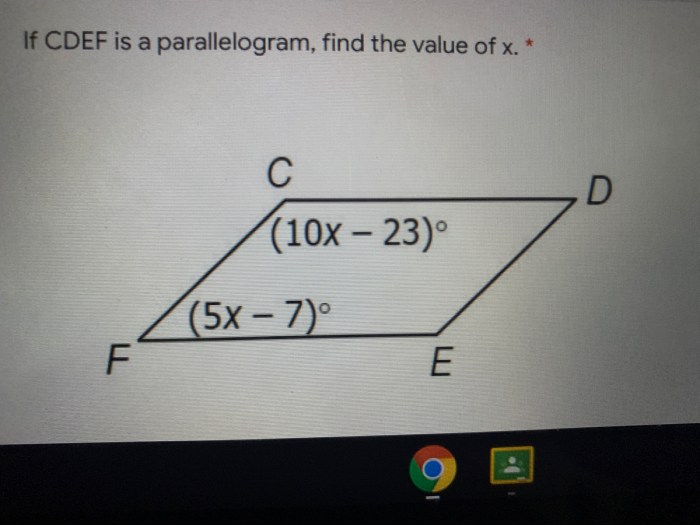
In a parallelogram, the opposite angles are congruent. Therefore, to find the measure of angle FCD, we can find the measure of its opposite angle, angle ECD.

Formula for FCD

The sum of the interior angles of a parallelogram is 360 degrees. Let’s assume the measure of angle ECD is x. Then, we have:“`∠ECD + ∠EDC + ∠DCF + ∠FCD = 360°x + 90° + 90° + x = 360°“`Solving for x, we get:“`

• x + 180° = 360°
• x = 180°

x = 90°“`Therefore, the measure of angle FCD is also 90 degrees.

Sample Parallelogram

Consider the parallelogram ABCD below:[Image of a parallelogram with labeled angles ECD, EDC, DCF, and FCD]In this parallelogram, we can see that angle ECD and angle FCD are opposite angles. Therefore, they are congruent. Since the measure of angle ECD is 90 degrees, the measure of angle FCD is also 90 degrees.

General Inquiries

What is the definition of a parallelogram?

A parallelogram is a quadrilateral with opposite sides parallel and congruent.

How can I identify if a quadrilateral is a parallelogram?

Check if the opposite sides are parallel and congruent, or if the opposite angles are congruent.

What is the relationship between the diagonals of a parallelogram?

The diagonals of a parallelogram bisect each other.