Embark on a mathematical journey with the Distance and Midpoint Puzzle Answer Key, an essential guide to unlocking the secrets of geometric calculations. This comprehensive resource provides a clear understanding of the distance and midpoint formulas, empowering you to solve puzzles and navigate real-world applications with confidence.

Delve into the fascinating world of geometry, where distances and midpoints play a crucial role in defining shapes, measuring lengths, and determining positions. Discover the power of these formulas and their versatility in various fields, from physics to engineering.

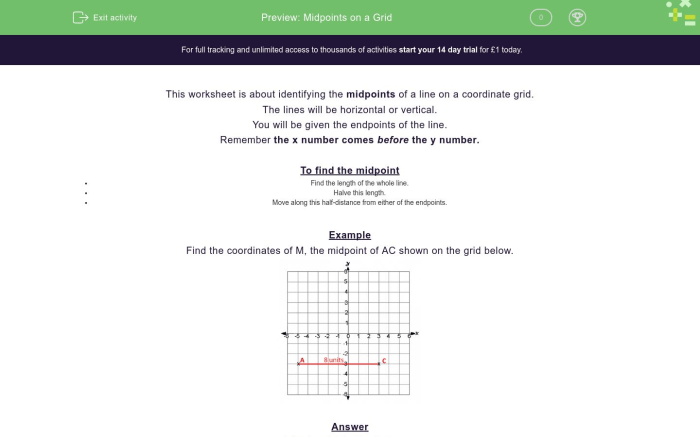
Distance and Midpoint Puzzle Answer Key

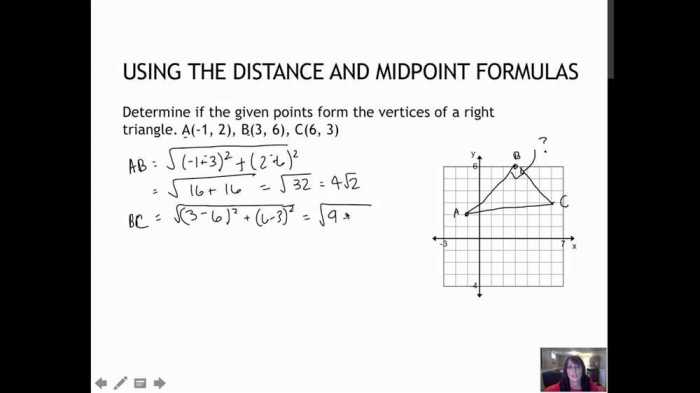
This document provides a comprehensive overview of distance and midpoint formulas, including examples and applications. It also includes a puzzle involving distance and midpoint calculations, along with a step-by-step solution.

Distance Formula

The distance formula calculates the distance between two points in a coordinate plane. It uses the coordinates (x1, y1) and (x2, y2) of the two points to calculate the distance d as follows:

d = √((x2

• x1)² + (y2
• y1)²)

For example, to calculate the distance between the points (2, 3) and (5, 7), we can use the distance formula as follows:

d = √((5

• 2)² + (7
• 3)²)

= √(3² + 4²)= √(9 + 16)= √25= 5

Midpoint Formula, Distance and midpoint puzzle answer key

The midpoint formula calculates the midpoint of a line segment connecting two points in a coordinate plane. It uses the coordinates (x1, y1) and (x2, y2) of the two points to calculate the midpoint (x_m, y_m) as follows:

x_m = (x1 + x2) / 2y_m = (y1 + y2) / 2

For example, to calculate the midpoint of the line segment connecting the points (2, 3) and (5, 7), we can use the midpoint formula as follows:

x_m = (2 + 5) / 2 = 3.5y_m = (3 + 7) / 2 = 5

Therefore, the midpoint of the line segment is (3.5, 5).

Distance and Midpoint Puzzle Examples

Puzzle: Find the distance between the points (1, 2) and (5, 6), and the midpoint of the line segment connecting them.

Solution:1.

-*Distance

Using the distance formula, we have:

d = √((5

• 1)² + (6
• 2)²)

= √(4² + 4²)= √(16 + 16)= √32= 5.66

Therefore, the distance between the points (1, 2) and (5, 6) is 5.66.2.

-*Midpoint

Using the midpoint formula, we have:

x_m = (1 + 5) / 2 = 3y_m = (2 + 6) / 2 = 4

Therefore, the midpoint of the line segment connecting the points (1, 2) and (5, 6) is (3, 4).

FAQ

What is the distance formula?

The distance formula calculates the distance between two points (x1, y1) and (x2, y2) using the formula: distance = √((x2 – x1)² + (y2 – y1)²).

How do I find the midpoint of a line segment?

The midpoint formula determines the midpoint ((x1 + x2)/2, (y1 + y2)/2) of a line segment with endpoints (x1, y1) and (x2, y2).