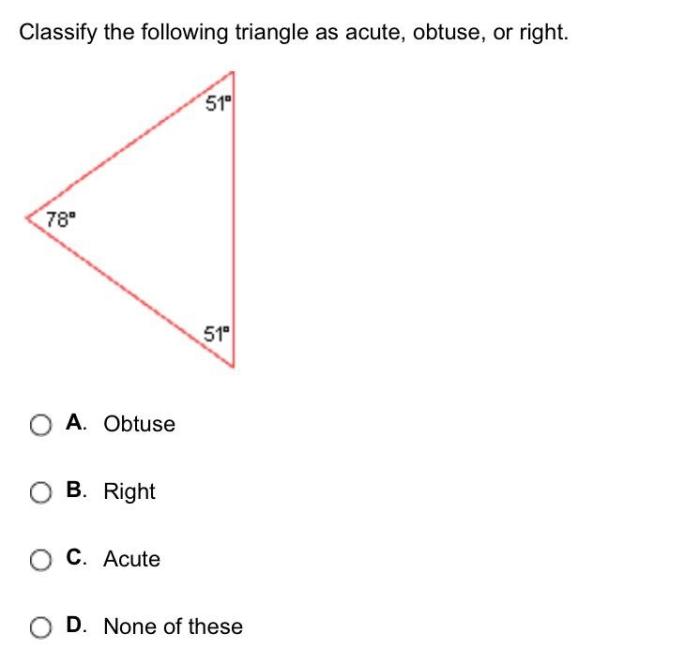
Classify the following triangle as acute obtuse or right – In the realm of geometry, triangles stand out as captivating shapes with unique characteristics. Classifying triangles as acute, obtuse, or right is a fundamental concept that forms the cornerstone of understanding their properties and applications. This exploration delves into the intricacies of triangle classification, empowering learners with the knowledge to distinguish these shapes with precision.
Triangles are defined by their three sides and three angles, with each angle measuring less than 180 degrees. Acute triangles boast angles that are all less than 90 degrees, while obtuse triangles possess one angle greater than 90 degrees. Right triangles, on the other hand, are characterized by one angle that measures exactly 90 degrees.
1. Definition of Acute, Obtuse, and Right Triangles
Triangles are classified into three main types based on the measure of their interior angles: acute, obtuse, and right triangles.
An angle is formed when two lines intersect at a point. The measure of an angle is expressed in degrees, with a full circle measuring 360 degrees.
An acute triangle is a triangle with all three interior angles measuring less than 90 degrees. An obtuse triangle is a triangle with one interior angle greater than 90 degrees. A right triangle is a triangle with one interior angle exactly equal to 90 degrees.
2. Properties of Acute, Obtuse, and Right Triangles: Classify The Following Triangle As Acute Obtuse Or Right
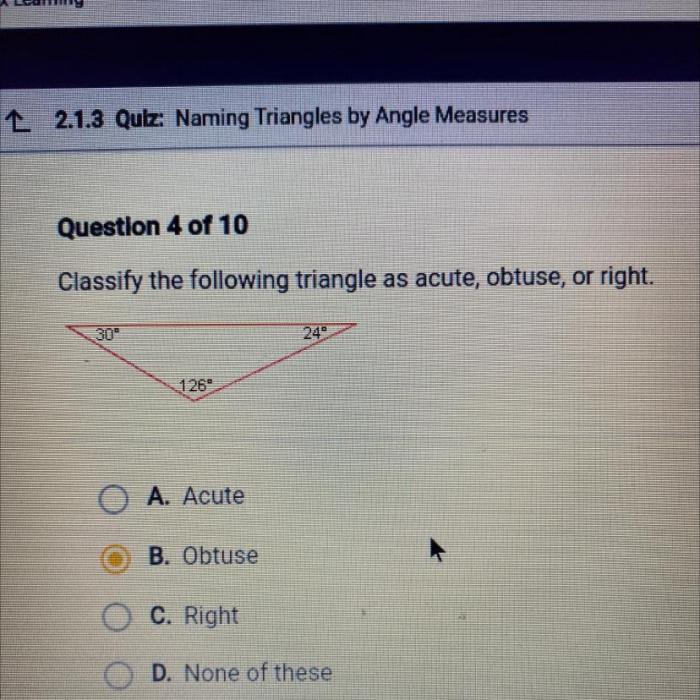
Acute Triangles, Classify the following triangle as acute obtuse or right
Acute triangles have certain properties that distinguish them from other types of triangles. The sum of the interior angles of an acute triangle is always less than 180 degrees. The longest side of an acute triangle is always opposite the largest angle.
Obtuse Triangles
Obtuse triangles also have unique properties. The sum of the interior angles of an obtuse triangle is always greater than 180 degrees. The longest side of an obtuse triangle is always opposite the obtuse angle.
Right Triangles
Right triangles have special properties that make them useful in many applications. The Pythagorean theorem, which states that the square of the hypotenuse (the longest side) of a right triangle is equal to the sum of the squares of the other two sides, is a fundamental property of right triangles.
Right triangles also have trigonometric ratios, which are ratios of the lengths of the sides of the triangle. These ratios are used to solve problems involving angles and distances.
3. Methods for Classifying Triangles
Triangles can be classified using various methods. The most common method is to measure the interior angles of the triangle using a protractor or other angle-measuring device.
If all three interior angles measure less than 90 degrees, the triangle is acute. If one interior angle measures greater than 90 degrees, the triangle is obtuse. If one interior angle measures exactly 90 degrees, the triangle is right.
Another method for classifying triangles is to use the Pythagorean theorem. If the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, the triangle is right.
4. Examples of Triangle Classification

| Triangle Type | Angle Measurements | Classification |
|---|---|---|
| Acute | 60°, 70°, 50° | Acute |
| Obtuse | 95°, 45°, 40° | Obtuse |
| Right | 90°, 45°, 45° | Right |
These examples illustrate the different types of triangles and their corresponding angle measurements and classifications.
Commonly Asked Questions
What is the difference between an acute and an obtuse triangle?
Acute triangles have all angles less than 90 degrees, while obtuse triangles have one angle greater than 90 degrees.
How can I classify a triangle using its side lengths?
You can use the Pythagorean theorem to determine if a triangle is a right triangle. If the square of the length of the longest side is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right triangle.
What are the properties of right triangles?
Right triangles have many special properties, including the Pythagorean theorem, the trigonometric ratios, and the fact that the sum of the squares of the lengths of the two shorter sides is equal to the square of the length of the longest side.