Which statements are true about the linear inequality y 3/4x-2 – Which statements are true about the linear inequality y ≥ 3/4x – 2? This question delves into the realm of linear inequalities, providing a comprehensive understanding of their properties, applications, and significance. Linear inequalities are mathematical expressions that represent relationships between variables, defining regions and boundaries that shape our understanding of various real-world phenomena.
To fully grasp the concept of linear inequalities, we will explore the specific inequality y ≥ 3/4x – 2, examining its slope, y-intercept, boundary line, and the region it defines. We will demonstrate how to graph this inequality, providing a visual representation of its solution set.
Furthermore, we will uncover the practical applications of linear inequalities in diverse fields, showcasing their power in modeling real-world scenarios.
Linear Inequalities: y ≤ 3/4x
2
2
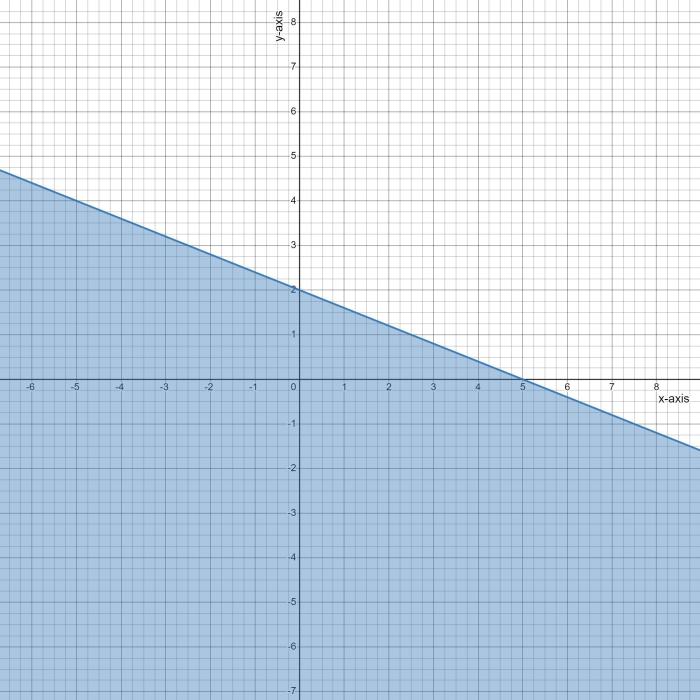
Linear inequalities are mathematical expressions that represent the relationship between two variables, typically x and y, in the form y ≤ mx + c, where m is the slope and c is the y-intercept. The inequality symbol ≤ indicates that y is less than or equal to the expression on the right-hand side.
Slope and y-Intercept
The slope of the line represented by the inequality y ≤ 3/4x – 2 is 3/4, which indicates the rate of change in y for a unit change in x. The y-intercept is -2, which is the point where the line intersects the y-axis.
Boundary Line and Solution Region
The boundary line is the line represented by the equation y = 3/4x – 2. The inequality symbol ≤ indicates that the solution region is below the boundary line. Points on the boundary line satisfy the equation y = 3/4x – 2, while points below the boundary line satisfy the inequality y ≤ 3/4x – 2.
Examples of Ordered Pairs, Which statements are true about the linear inequality y 3/4x-2
Some examples of ordered pairs that satisfy the inequality y ≤ 3/4x – 2 are:
- (0, -2): This point lies on the boundary line.
- (1, -1): This point lies below the boundary line and satisfies the inequality.
- (2, 0): This point lies below the boundary line and satisfies the inequality.
Graphing the Linear Inequality
To graph the linear inequality y ≤ 3/4x – 2, follow these steps:
- Plot the boundary line y = 3/4x
2 as a solid line.
- Shade the region below the boundary line, as this region represents the solution to the inequality.
Applications in Real-World Scenarios
Linear inequalities have numerous applications in real-world scenarios, including:
- Finance:Calculating the maximum amount of money that can be borrowed based on income and expenses.
- Economics:Determining the production levels that maximize profit.
- Science:Modeling the relationship between variables in physical phenomena.
Feasible Region
When multiple linear inequalities are combined, the feasible region is the area that satisfies all the inequalities simultaneously. Finding the feasible region involves graphing each inequality and identifying the common region that satisfies all the conditions.
Detailed FAQs: Which Statements Are True About The Linear Inequality Y 3/4x-2
What is the slope of the boundary line for the inequality y ≥ 3/4x- 2?
3/4
What is the y-intercept of the boundary line for the inequality y ≥ 3/4x- 2?
-2
Is the point (2, 3) in the solution region of the inequality y ≥ 3/4x- 2?
Yes